UJI ASUMSI KLASIK PART 2
Setelah sebelumnya saya membahas tentang linearitas dan multikolineritas pada Uji Asumsi Klasik Part 1, kali ini saya akan membahas uji normalitas, uji heteroskedastisitas, dan uji autokorelasi yang merupakan bagian dari uji asumsi klasik.
Sebelum membahas jauh ketiga uji tersebut, saya ingin menjelaskan kembali pentingnya uji asumsi klasik. Uji asumsi klasik adalah uji yang dilakukan sebelum pemrosesan data regresi (baik sederhana atau berganda) agar persamaan yang dihasilkan memenuhi kaidah Best linear Unbias Estimator. Jika uji asumsi klasik tidak dilakukan sebelum pemrosesan data, persamaan yang dihasilkan diragukan kemampuannya dalam menghasilkan prediksi yang akurat.
UJI NORMALITAS
Secara sederhana uji normalitas ini bertujuan agar residu yang dihasilkan dari selisih antara Y aktual dan Y prediksi terdistribusi dengan normal. Mengapa harus normal? Kriteria distribusi normal biasanya digunakan untuk analisis parametrik yang menggunakan data rasio atau interval. Jika data galat / residunya terdistribusi normal, maka sangat mudah untuk menentukan tingkat kepercayaan dengan α = 0.05 atau 0.1. Tingkat kepercayaan yang diperoleh harus akurat mengingat data parametrik biasanya menggunakan data yang sangat sensitif. Misal data pertumbuhan bakteri terhadap suatu penyakit, atau contoh lainnya.
Mari kita langsung praktekkan uji tersebut
Langkah pertama adalah menentukan nilai residu. Nilai residu diperoleh dari selisih nilai Y aktual dengan Y prediksi. Berikut adalah data yang saya miliki;
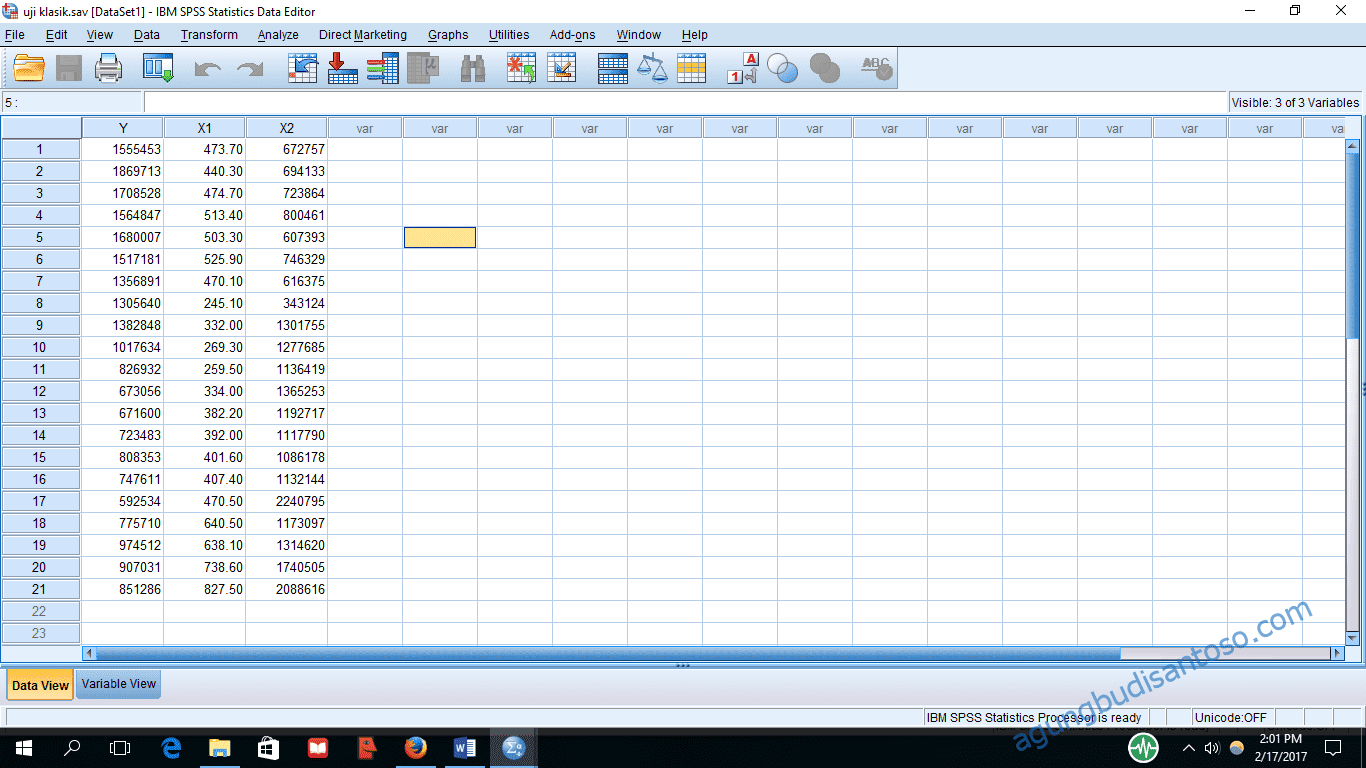
Pilih Analyze-Regression-linear
Masukkan nilai Y ke variabel dependent, dan varabel X1 dan X2 ke variable independenst(s)
Klik tombol save, kemudian pilih unstandardized pada tab residual, klik continue
Klik Ok dan tunggu hasilnya, worksheet terlihat terdapat variabel baru yakni RES_1
Kemudian kita akan menggunakan data tersebut untuk mengetahui apakah nilai residu terdistribusi normal atau tidak dengan menggunakan uji kolgomorov-smirnov
Pilih menu Analyze-non parametric test-one sample
Pilih variabel yang akan disubmit ke tab field. Boleh variabel Res_1 saja, atau keseluruhan. Disini saya masukkan keseluruhan karena analisisnya nanti satu satu/terpisah. Kemudian klik run.
Tunggu hasilnya
Terlihat pada baris ke empat bahwa residul terdistribusi normal dengan significant level 0.05 atau terima H0
UJI HETEROSKEDASTISITAS
Uji ini digunakan untuk melihat apakah terdapat ketidaksamaan varian dari residu pengamatan yang satu ke pengamatan lainnya. Ribet ya bacanya… 🙂 . Jika timbul ketidaksamaan, maka disebut gejala heteroskedastisitas.
Begini, regresi menghendaki adanya keteraturan varian dari residu. Atau malah bisa dibilang mestinya varian residu itu sama/konstan. Jika variannya berbeda beda maka itu yang disebut heteroskedastisitas. Karena variannya beragam, dikhawatirkan nantinya nilai Y prediksi tidak konsisten atau bias.
Langsung kedalam praktek…
Kita masih menggunakan variabel Res_1 yang digunakan uji normalitas diatas, namun kita gunakan nilai mutlaknya (tidak ada nilai negativ). Caranya?
Pilih menu transform-compute variable
Kemudian dengan menggunakan fungsi absolut (abs) kita membuat variabel baru bernama abs_1
Hasilnya
Kemudian kita meregresikan variabel abs_1 sebagai variabel dependen (Y) dan variabel X1 dan X2 sebagai variabel independennya.
Hasil yang diperoleh
Terlihat dari nilai F dan R Squared bahwa pengaruh bebas tidak signifikan menjelaskan variasi yang terjadi pada variabel dependen (dalam hal ini nilai absolut residunya) sehingga dikatakan tidak memiliki gejala heteroskedastisitas.
Oh iya, uji yang kita gunakan ini namanya uji glejser.
UJI AUTOKORELASI
Autokorelasi adalah korelasi (hubungan) yang terjadi diantara serangkaian pengamatan yang tersusun secara waktu yang biasanya terjadi pada data timeseries. Jika ternyata variabel t atau t-1 (dibaca: peride waktu) ternyata mempengaruhi nilai Y, maka inilah yang disebut sebagai autokorelasi. hal ini biasanya dicirikan dengan nilai atau grafik residualnya memiliki pola misal linear atau berzigzag sesuai siklus tertentu. Artinya???? Artinya besar kemungkinan analisis yang tepat untuk menggambarkan persamaan tersebut adalah analisis time series. Jika anda tetap ingin menggunakan regresi sebagai alat analisis, sebaiknya memasukkan time sebagai variabel independen. Arti time dimasukkan sebagai variabel independen bukan berarti waktu “tahun” yang dimasukkan, malainkan ada unsur Y-1 sebagai variabel independen atau istilah statistiknya lag-1, lag-2, dst. Itu merupakan tehnik yang paling sederhana.
Langsung ke cara aplikatifnya.. Kita akan menggunakan nilai Durbin-Watson.
Pilih analyze-regression-linear
Kemudian klik tombol statistic setelah memasukkan variabel Y dan X nya
Centang durbin-watson dan klik continue
Klik OK dan tunggu proses
Kita memperoleh nilai durbin watson = 1.248
Kita bisa mengartikan nilai Durbin Watson sebagai berikut:
- jika pengujian diperoleh nilai DW statistik di bawah -2, maka diindikasikan ada autokorelasi positif
- jika pengujian diperoleh nilai DW statistik diantara -2 sampai 2, maka diindikasikan tidak ada autokorelasi
- jika pengujian diperoleh nilai DW statistik diatas 2, maka diindikasikan ada autokorelasi negatif.
Jika diperoleh hasil durbin watson = 1.248, terlihat bahwa tidak ada autokorelasi pada data yang saya gunakan.
Terima kasih telah berkunjung.
Assalamualaikum bapak, saya iis mau bertanya, saat saya melakukan uji asumsi klasik, nilai residual yang muncul adalah 0 dan nilao dirbin watsonnua sangat tinggi. Saya menggunakan data sekunder dengan time series, kira kira kesalahan saya terleta dimana ya? Karena saya belum pernah mendapatkam kondisi seperti itu, terima kasih
wa aalaikum salam. durbin watson yang tinggi menandakan adanya auto korelasi. hal ini terjadi karena mbk menggunakan data time series. biasanya untuk menghilangkan autokorelasi, menggunakan differencing. terima kasih
Assalmualaikum bapak.. saya mau bertanya data saya setelah di tranformasi normal namun terjadi autokorelasi, bagaimana cara mengatasinya bapak?
wa alaikum salam mbk.. autokorelasi umumnya disebabkan karena menggunakan variabel time series. cara mengatasinya? jika datanya berupa data panel, maka sebaiknya analisis regresi panel, tapi jika bukan, maka hilangkan trend terlebih dahulu dalam variabel tersebut. terima kasih
Terima kasih mas.. Mencerahkan..
tulisan yg menarik.
Terima kasih sudah berkunjung om dro..