Uji linearitas adalah salah satu uji asumsi klasik yang dilakukan untuk mengetahui sifat linear pada sebaran data antara variabel X dan Y. Perlunya mengetahui adakah sifat linear pada hubungan X dan Y mempengaruhi tingkat valid atau tidaknya model regresi yang dihasilkan. Jadi, sebagus apapun model regresi yang dihasilkan dengan R squared yang tinggi, namun jika data tersbeut tidak memiliki sifat linear, maka kemungkinan akan terjadi kesalahan estimasi.
Mengapa Perlu uji linearitas?
Pada dasarnya regresi dibentuk dengan dasar linear. Karena model regresi pada umumnya adalah
Y prediksi = a + bx, sedangkan
Y aktual = a + bx + error
Error merupakan selisih antara Y prediksi dan Y aktual. Jika model itu tepat dalam menginterpretasikan Y aktual, maka dikehendaki error akan semakin kecil. Error kecil akan ditunjukkan dengan melihat R squared. Karena semakin tinggi R squared maka akan mencerminkan model akan baik. Satu hal yang bisa kita simpulkan adalah ciri model tersebut memenuhi sifat linearitas adalah nilai R squarednya tinggi.
Tapi, ternyata belum tentu R squared tinggi pasti linearitas akan terpenuhi. Hal ini bisa disebabkan karena ada kemungkinan nilai error yang kecil pada sisa R squared ternyata membentuk pola yang tidak linear. Bingung? Perhatikan contoh berikut:
Misalkan ada model regresi dengan R squarednya 70%, yang artinya 70 persen dari data yang diberikan, dapat diproyeksikan dengan tepat oleh model yang dihasilkan regresi. Mungkin kita akan berpikir, sudah cukup linear karena sudah mengakomodir data sebesar 70%. Namun, ternyata 30 persen sisanya (error) membentuk pola kuadratic yang sangat berbeda dari model regresinya. Ketika di uji linearitas pun ternyata tidak linear. Nanti dibagian akhir artikel ini akan dibahas.
Cara menentukan linearitas menggunakan SPSS
Sebelum membahas apa yang sudah saya sebutkan tadi, mungkin ada yang belum paham bagaimana cara mengetahui linearitas data. Pada artikel uji asumsi klasik, sudah saya terangkan menghitung uji linearitas dengan menggunakan perhitungan manual. Sedangkan perhitungan dengan SPSS ada pada menu analyze – compare means – means. Kemudian pada windows yang muncul isikan variabel Y sebagai dependen varaibel, dan variabel X sebagai independen variabel. Klik tombol option dan beri centang pada test for linearity.

Saya dalam artikel ini tidak akan membahas secara detil bagaimana cara melakukan test linearitas pada SPSS, karena saya lihat di blog yang lain sudah dijelaskan langkah demi langkah. Namun, saya akan sedikit mengkoreksi penjelasan yang sedikit keliru, yakni pada saat membaca hasil atau tabelnya.

Banyak yang menjelaskan bahwa linearitasnya ditentukan oleh diviation from linearity. Jika diatas 0.05 maka dikatakan memenuhi kaidah linear. Hal itu memang benar tapi belum komplit. Kita sebaiknya melihat tabel itu secara utuh. Pertama, kita melihat nilai significant pada linearity. Jika nilai ini dibawah 0.05, menandakan bahwa benar ada hubungan linear antara variabel X dan variabel Y.
Selanjutnya pada “deviation from linearity” yang dimaksud adalah apakah ada pola linear dari error (dalam hal ini diistilahkan deviasi) dalam model linear tersebut. Jika nilai signifikannya dibawah 0.05 berarti benar ada hubungan linear pada error di model linear antara X dan Y. inilah kenapa nilai signifikan disini kita harapkan diatas 0.05. karena pada kondisi linearitas seharusnya tidak ada lagi pola linear pada deviasi atau error.
Jadi arti tabel diatas adalah ada pola linear pada hub X dan Y dan tidak ada pola linear pada deviation from linearity, sehingga dikatakan memenuhi persyaratan linearitas.
Apakah ada x dan y memiliki hubungan linear tapi errornya juga masih memiliki hub linear? Jawabnya ada. Silahkan perhatikan tabel dibawah ini:

Artinya pada X dan Y sudah memiliki hubungan linear tetapi masih menyisakan error yang juga masih berpola. Artinya kemungkinan hubungan X dan Y tersebut tidak mengakomodir semua data. Meskipun sedikit data yang sudah tidak bisa diterangkan, namun jika masih memiliki pola tertentu, besar kemungkinan ada model lain yang lebih tepat untuk menjelaskan keseluruhan data.
Hubungan R squared dengan sifat linearitas
Pada pembukaan awal tadi saya katakan bahwa belum tentu nilai r squared tinggi memiliki sifat linearitas. Perhatikan tabel output uji linearitas dibawah ini:
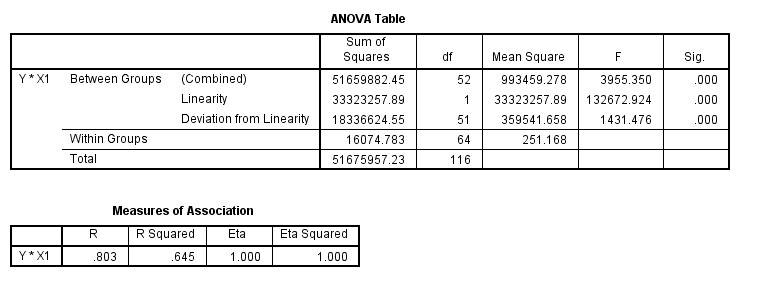
R squared pada model diatas adalah 0.645 yang sudah cukup baik merepresentasikan data karena 60 persen sudah dapat dijelaskan. Namun perhatikan signifikan pada uji linearitas ternyata tidak linear. Hal ini mengindikasikan bahwa error pada model sebesar 0.355 memiliki pola tertentu. Untuk membuktikan ini, kita bisa melakukan plot X dan Y dan hasilnya sebagai berikut:

Ternyata hubungan pola x dan Y bersifat kuadratic, dan kemungkinan error term terletak pada saat x =0 hingga titik puncak minimum kurva tersebut. Sedangkan model regresinya menjelaskan titik minimum hingga X =4000.
Kesimpulan yang diperoleh dari artikel ini adalah bahwa r squared yang tinggi belum tentu menjelaskan terpenuhinya sifat linearitas. Kemudian transformasi data yang sifatnya meniinggikan r squared perlu di periksa ulang apakah transformasi data tersebut mampu mengubah pola hubungan menjadi linear atau tidak.
Tujuan linearitas pada regresi adalah meyakinkan hubungan slinear pada x dan y dan juga dampak dari model tersebut. Sifat linear tidak hanya antara x dan Y saja, namun diharapkan error yang tersisa sudah tidak memiliki pola tertentu sehingga memastikan bahwa model yang dikeluarkan benar benar tepat.
Lalu bagaimana cara mengatasi data yang seperti ini? Yuk simak video tutorialnya akan dibahas lengkap.
assalamu’alaikum mas…
sebelumnya terimakasih atas ilmunyaaa
saya sudah mencoba ke 4 tranformasi data yang dicontohkan mas agung tetapi deviation of linearity nya masi kurang dari 0.05. apakah ada cara lain ya? soalnya pola data saya seperti mengumpul di tengah gitu mas saya jadi bingung😭 dan apakah jika data tidak linear masih dapat dilakukan uji hipotesis dan koefisien determinasi ?
mohon bantuannya mas, terima kasih🙏🏾
Coba dilihat dulu dari sisi normalitas untuk masing masing variabel. Lihat artikelnya di https://agungbudisantoso.com/tips-mengatasi-kendala-pada-uji-normalitas
Jika tidak memenuhi syarat linearitas,regresi masih bisa dilakukan dengan regresi nonlinear. Saya juga sudah bahas, cari di kategori regresi. Terima kasih.
assallamualaikum wr wb.
izin nanya om, kira2 apa penyebab deviasi from linierity bisa dibawah o,o5 padahal nilai linierity nya < 0,05 . dan apakah masi bisa lanjut untuk analisis jalur , saya menggunakan 1 variabel bebas 1 variabel intervening dan 1 terikat, terimaksih banyak
wa alaikum salam. jika ditanya penyebab, penyebabnya adalah data pencilan. sebaiknya diperbaiki terlebih dahulu sebelum ke analisis jalurnya ya mas… terima kasih
Permisi mohon maaf mengganggu pak,
Saya Putri hendak bertanya, apabila kasus saya sama dengan data tidak linier, lalu sudah mencoba trik transformasi data yang bapak berikan, tapi tetap 0.000, lalu saya coba saya pangkalan 4 baru dapat linear, itu bagaimana ya pak solusinya?
Apakah menyalahi aturan transform data atau memang data saya sudah sangat tidak linear ya pak? Terimakasih
untuk menjawab. coba gunakan scatter plot dan amati apakah data mbk memang sudah sangat tidak linear ya… terima kasih
Selamat malam Pak.
Saya melakukan uji linearitas. Menggunakan 2 variabel X. Dan salah satu variabel x saya tidak linear. Apa yang harus saya lakukan terhadap masalah tersebut???
Terimakasih
Coba lakukan regresi non linear mas. Terima kasih
Saya mau bertanya saya melakukan uji Normalitas dan hasilnya tidak normal kemudian saya outlier dengan metode z-score. Hasilnya sudah normal. Kemudian saya gunakan data yg yg sudah dioutlier untuk uji linieritas, hasilnya tidak linier. Terus saya pakai uji nonlinear. Yang dilihat R quare atau nilai sig nya. Untuk variabel X1 nilai R Quare besar di model quadratik namun sig diatas 0.05. Untuk variabel X2 nilai R square lebih besar di kuadratik dan sig lebih kecil 0.05 dibanding yg lain. Untuk X3 nilai R square lebih besar di kuadratik namun nilai sig <0.05 ada di model linier. Jadi bagaimana jika seperti itu?
pertanyaan saya, mengapa anda melakukan regresi sederhana ya? seharusnya ketiga variabel tersebut di run bersamaan (regresi berganda). karena seharusnya r square untuk kesemuanya hanya ada satu.
Assalamualaikum pak Agung, saya izin bertanya jika sig linearitas <0,05. Tetapi sig pada deviaton from linearity <0,05. Itu artinya apa ya pak? Karna sig linearitas saya nilai nya 0,000. Sedangkan sig deviaton from linearity nya hasil nya 0,039. Mohon bantuan nya pak.. terimakasih
sepertinya ini sudah dibahas di artikelnya ya… ayo yang semangat bacanya…
pak, bagaimana jika sig. <0.001? apa itu bisa dilanjutkan?
Itu artinya masih dibawah 5 persen
apakah linierity test juga diperlukan untuk regresi berganda ?
tepat sekali. diperlukan di linear berganda. terima kasih
Untuk penggunaan Linearity Sig 0,05, Sumber bukunya dari mana ya Pak\? Terima kasih
di uji linieritas katanya perlu melihat f tabel dan f hitung, itu maksudnya gmana ya pak?
nilai besar f hitung dan f tabel sudah tercover jika melihat nilai signifikan. klo bahasa Ho dan H1 memang perlu ada bahasa f hitung dan f tabel.
Assalamualaikum, pak. Saya ingin bertanya, penelitian saya menggunakan variabel mediasi dan saat pengujian saya memasukkan variabel Z ke factor list bersama dengan variabel Y. Hasil yang saya dapatkan ada 2 tabel, tabel pertama antara X.Y sudah memiliki nilai sig. linearity <0.05, tapi nilai deviation of linearitynya 0.015, dimana masih terdapat error, nilai R kuadratnya 0.196.
Lalu pada tabel X.Z, nilai sig. linearitynya juga <0.05, tetapi nilai deviation of linearitynya 0.034, dengan r kuadrat 0.128.
Ini solusinya bagaimana ya pak? Karena data saya sudah memiliki hubungan, tetapi masih terdapat pola yang error dan juga R kuadratnya juga tidak besar. Mohon bantuan dan sarannya, pak
wa alaikum salam.. kembalikan ke teori dulu athiyah. apakah memang variabel xyz itu secara teori memang ada pengaruh yang signifikan, ataukah athiyah memiliki data random?
jika dirasa proses penelitiannya sudah betul, saatnya membaca literatur apakah ada yang mengalami kasus sama ataukah berbeda.
tapi jika memang harus dipaksa untuk naik r squarenya maka baiknya tambah variabel. terima kasih
Selamat malam pak, saya mahasiswa smt akhir sedang melakukan analisis data menggunakan spss
Sejauh pengisian data di setiap variabel hasil tersebut ok namun ada 1 uji di salah satu variabel nilai signifikansinya <0,05 yg mana di peroleh hasil sig 0,007 dengan nilai F 2,958
cara menjelaskannya gmana pak ? Kalo olah data ulang otomatis berubah semua 😂
informasi yang mas hadirkan hanya bisa menjawab jika variabel tersebut signifikan mempengaruhi variabel dependennya. besar nilai pengaruhnya tergantung nilai koefisien variabel tersebut. terima kasih
Assalamu’alaikum Pak Agung, jika bentuk diagram hasil output linearitas tidak berpola seperti yg bapak contohkan, maka bagaimana cara mengatasinya ya Pak? Pola saya misah atau berpencar gitu Pak …
Mohon bantuannya ya Pak terimakasih 🙏
Wa alaikum salam mbak. Maka bisa gunakan non linear atau gunakan ln untuk mengupayakan bisa linear. Oh iya, jangan lupa lihat video yutubnya di artikel tersebut karna saya mendemokan salah satu solusinya. Terima kasih.
Assalamualaikum Mas Agung,
Saya sudah lihat videonya, hanya terlalu cepat dan kurang detail cara dan penjelasannya….kalau saya mau bertanya….ditujukan ke alamat email mana?
Terima kasih
Silahkan hub saya lewat a.budisantoso058@gmail.com
Sudah saya email Ya Pak. Matur suwun