Salah satu uji asumsi klasik yang harus dipenuhi pada analisis regresi adalah multikolinearitas. Multikolinearitas adalah suatu kondisi pada model regresi yang memiliki variabel independen saling berhubungan sedang atau kuat. Hubungan atau korelasi sedang dan kuat biasanya ditentukan dengan nilai korelasi masing masing variabel.
Seperti yang kita ketahui korelasi dan regresi memiliki tingkatan yang berbeda. Korelasi menyatakan hubungan tetapi tidak saling mempengaruhi satu sama lain. Sedangkan regresi memiliki variabel yang mempengaruhi dan variabel yang dipengaruhi. Jadi pada korelasi belum ditentukan mana variabel yang mempengaruhi dan mana yang dipengaruhi, artinya kedua variabel pada posisi yang sama.
Multikolinearitas akan muncul jika salah satu atau beberapa diantara variabel memiliki korelasi. Penyakit multikolinearitas ini akan semakin besar dampaknya jika antara variabel memiliki tingkat pengaruh atau regresi di dalam regresi. karena tingkatan regresi lebih tinggi dibandingkan korelasi seperti yang dijelaskan di paragraf sebelumnya.
Dampak Multikolinearitas
Multikolinearitas memiliki dampak yang cukup besar. Setidaknya ada dua dampak yang akan dirasakan mengganggu hasil dari regresi berganda. Pertama, nilai signifikansi akan tidak valid atau menurun. Kedua, nilai koefisien bertentangan dengan teori. Agar dapat dipahami dengan mudah dampak dari multikolinear ini, mari kita belajar bersama memahami multikolinearitas dengan menggunakan data di bawah ini:
jika data diatas kita run dengan regresi berganda dengan X1 dan X2 sebagai variabel independen, dan Y sebagai variabel dependen dengan menggunakan SPSS. Guna memunculkan indikasi multikolinearitas, klik statistic dan beri centang collinierity diagnostic:

klik continue dan klik OK. maka akan muncul hasil sebagai berikut:

terlihat pada gambar diatas hasil ini tidak signifikan secara parsial baik X1 maupun X2 karena memiliki nilai signifikansi yang lebih besar dari 0.05. Hal ini akan dirasakan mengherankan jika secara teori X1 dan X2 seharusnya memiliki pengaruh yang kuat terhadap nilai Y.
Dengan data yang sama coba kita regresikan sekali lagi dengan Y sebagai variabel dependen dan X1 sebagai variabel independen. hasilnya adalah sebagai berikut:
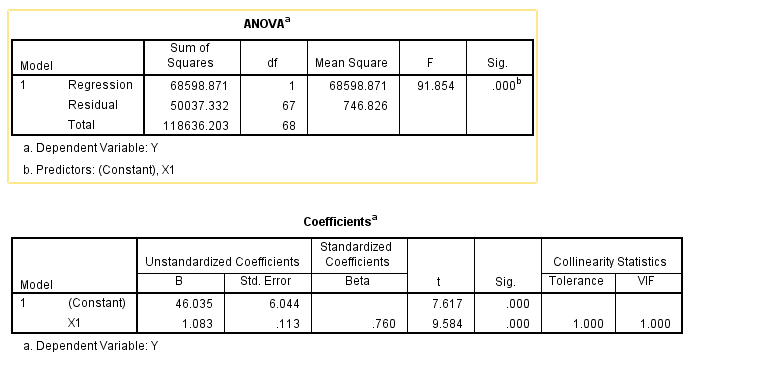
terlihat pada gambar diatas, X1 memiliki pengaruh yang kuat terhadap Y yang dibuktikan dengan nilai signifikansi dibawah 0.05 dengan koeffisien positif. Kemudian kita lakukan hal yang sama terhadap X2 (Y sebagai variabel dependen dan X2 sebagai variabel independen). hasilnya adalah sebagai berikut:

Sama seperti X1, X2 seharusnya memiliki pengaruh yang kuat terhadap variabel Y. Lalu, mengapa jika digabungkan keduanya malah tidak signifikan? betul, jawabnya karena terjadi multikolinearitas. untuk membuktikannya mudah saja, yakni dilihat dari nilai VIF pada gambar pertama diatas. Jika nilai VIF di atas 10, maka dapat diduga terjadi multikolinearitas. Gambar diatas memiliki nilai VIF diatas 100, yang artinya multikolinearitasnya sudah sangat kuat.
Oke, dampak pertama sudah terbukti yakni nilai signifikansinya menurun. lalu bagaimana dengan dampak kedua yakni perubahan pada nilai koefisien. Kembali perhatikan gambar 1 diatas. Koefisien X2 pada hasil tersebut memiliki nilai negatif. Arti nilai negatif pada tabel tersebut menandakan hubungan antara X2 dan Y. Semakin tinggi nilai X2 maka nilai Y2 semakin rendah (slope negatif).
Namun perhatikan pada gambar 3 pada saat X2 diregresikan secara terpisah dengan Y. Pada signifikan dibawah 0.05, terlihat bahwa hubungan X2 dan Y sebenarnya adalah positif. Untuk lebih jelasnya perhatikan kedua grafik X1 terhadap Y dan X2 terhadap Y dibawah ini:


Kedua grafik diatas memperlihatkan jika kedua variabel X1 dan X2 sebenarnya memiliki hubungan slope positif dengan Y jika diregresikan secara terpisah. Hal ini membuktikan bahwa multikolinearity bisa menyebabkan perubahan arah slope variabel independen pada regresi.
Jadi, jika anda menemukan hasil regresi yang tidak sesuai dengan teori. Misalkan penggunaan pupuk organik seharusnya memiliki koefisien positif terhadap produksi, tetapi mengapa terjadi koefisien negatif. Kemungkinan variabel pupuk organik tersebut memiliki korelasi dengan variabel independen lainnya seperti luas lahan, karena banyaknya penggunaan pupuk sangat bergantung kepada luas lahan yang dimiliki. Kasus ini sering terjadi terhadap data yang saya olah.
Solusi yang tepat untuk mengatasi multikolinear adalah mengeliminasi salah satu varaibel yang diindikasikan memiliki hubungan. pemeriksaan hubngan variabel variabel independen bisa dilakukan dengan menggunakan pearson correlation. Dalam SPSS bisa dijumpai pada menu analyze – correlate – bivariate.

terlihat pada gambar diatas X1 dan X2 memang memiliki korelasi yang sangat kuat. mengeliminasi salah satu keduanya akan memperbaiki multikolinearitas.
Solusi kedua dalam mengatasi multikolinearitas adalah tidak menggunakan OLS. Multikolinearitas merupakan salah satu kelemahan OLS yang biasa digunakan pada regresi. Biasanya jika anda menggunakan simultan, masalah multikolineraitas ini diabaikan karena simultan tidak menggunakan OLS, melainkan 2SLS.
VIF sebagai indikator multikolineritas
Banyak sumber yang menerangkan bahwa multikolinearitas bisa dilihat dari nilai VIF atau Variance Inflation Factor. jika nilai VIF diatas 10 maka mengindikasikan bahwa terjadi multikolinearitas.
Dalam artikel yang berjudul Variance Inflation Factor, rumus VIF adalah sebagai berikut:

R2 dalam rumus tersebut adalah koefisien determinansi antara salah satu variabel independen terhadap variabel independen lainnya. jika R2 bernilai 0, maka VIF akan bernilai 1, sebaliknya semakin kuat hubungan antar variabel atau koefisien determinansinya, maka nilai VIF juga akan semakin besar. Rumus ini juga dianggap sebagai invers dari toleransi hub antar variabel independen.
Jika kita buat grafik hubungan antara R2 dan nilai VIF adalah sebagai berikut:

Pada grafik itu terlihat bahwa jika nilai VIF 10, maka R2 sudah bernilai 90 persen atau lebih. Hal ini tentu mengindikasikan bahwa terjadi hubungan yang kuat antara salah satu variabel independen terhadap variabel independen lainnya.
Demikian, selamat belajar!
Tinggalkan Balasan